tdunn - Advent of Code 2021: Days 21-25

R setup

library(tidyverse)
library(gt)
library(tictoc)
library(lubridate)
theme_set(theme_minimal())

Python setup

library(reticulate)
use_virtualenv("r-reticulate")

import numpy as np
import pandas as pd
import timeit

Day 21: Dirac Dice

day21 <- read_lines("day21-input.txt")
day21 %>% str_trunc(70)

[1] "Player 1 starting position: 8" "Player 2 starting position: 1"

Part 1

There’s not much to do as you slowly descend to the bottom of the ocean. The submarine computer challenges you to a nice game of Dirac Dice.

This game consists of a single die, two pawns, and a game board with a circular track containing ten spaces marked 1 through 10 clockwise. Each player’s starting space is chosen randomly (your puzzle input). Player 1 goes first.

Players take turns moving. On each player’s turn, the player rolls the die three times and adds up the results. Then, the player moves their pawn that many times forward around the track (that is, moving clockwise on spaces in order of increasing value, wrapping back around to 1 after 10). So, if a player is on space 7 and they roll 2, 2, and 1, they would move forward 5 times, to spaces 8, 9, 10, 1, and finally stopping on 2.

After each player moves, they increase their score by the value of the space their pawn stopped on. Players’ scores start at 0. So, if the first player starts on space 7 and rolls a total of 5, they would stop on space 2 and add 2 to their score (for a total score of 2). The game immediately ends as a win for any player whose score reaches at least 1000.

Since the first game is a practice game, the submarine opens a compartment labeled deterministic dice and a 100-sided die falls out. This die always rolls 1 first, then 2, then 3, and so on up to 100, after which it starts over at 1 again. Play using this die.

The moment either player wins, what do you get if you multiply the score of the losing player by the number of times the die was rolled during the game?

player1 <- str_extract(day21[1], "position: \\d") %>% readr::parse_number()
player2 <- str_extract(day21[2], "position: \\d") %>% readr::parse_number()
player1; player2

[1] 8

[1] 1

Define a custom modulo function that returns 1-10 instead of 0-9:

custom_mod <- function(val) {
  ((val - 1) %% 10) + 1
}

Loop until a winner is found:

player1_score <- player2_score <- dice <- turn <- 0

while (player1_score < 1000 & player2_score < 1000) {
  turn <- turn + 1
  dice <- dice + 3
  
  roll <- sum(seq(dice, dice - 2))
  if (turn %% 2 == 1) {
    player1 <- custom_mod(player1 + roll)
    player1_score <- player1_score + player1
  } else {
    player2 <- custom_mod(player2 + roll)
    player2_score <- player2_score + player2
  }
}
player1_score; player2_score

[1] 1000

[1] 694

Multiply the turn number by 3 to get the number of dice rolls, then multiply that by the losing players score:

(turn * 3) * player2_score

[1] 518418

Python:

player1 = int(r.day21[0][-1])
player2 = int(r.day21[1][-1])

player1_score, player2_score, dice, turn = 0, 0, 0, 0

while player1_score < 1000 and player2_score < 1000:
  turn += 1
  dice += 3
  
  roll = sum(range(dice - 2, dice + 1))
  if turn % 2 == 1:
    player1 = ((player1 + roll - 1) % 10) + 1
    player1_score += player1
  else:
    player2 = ((player2 + roll - 1) % 10) + 1
    player2_score += player2

turn * 3 * player2_score

Part 2

Now that you’re warmed up, it’s time to play the real game.

A second compartment opens, this time labeled Dirac dice. Out of it falls a single three-sided die.

As you experiment with the die, you feel a little strange. An informational brochure in the compartment explains that this is a quantum die: when you roll it, the universe splits into multiple copies, one copy for each possible outcome of the die. In this case, rolling the die always splits the universe into three copies: one where the outcome of the roll was 1, one where it was 2, and one where it was 3.

The game is played the same as before, although to prevent things from getting too far out of hand, the game now ends when either player’s score reaches at least 21.

On each turn, the Dirac dice is rolled three times, leading to \(3 \times 3 \times 3 = 27\) permutations, i.e. 27 universes. However, the sum of these three rolls can only take on the following values:

roll_perm <- crossing(r1 = 1:3, r2 = 1:3, r3 = 1:3) %>%
  mutate(roll = r1 + r2 + r3) %>%
  count(roll)
roll_perm

# A tibble: 7 × 2
   roll     n
  <int> <int>
1     3     1
2     4     3
3     5     6
4     6     7
5     7     6
6     8     3
7     9     1

Define a function to roll the dice for a single player, but keep track of the states of the game (instead of each game individually), where a state is uniquely identified by the positions and scores of players 1 and 2.

roll_dirac <- function(players, player = 1) {
  players <- players %>% crossing(roll_perm)
  if (player == 1) {
    players <- players %>%
      mutate(pos1 = custom_mod(pos1 + roll), score1 = score1 + pos1,
             n_univ = n_univ * n)
  } else {
    players <- players %>%
      mutate(pos2 = custom_mod(pos2 + roll), score2 = score2 + pos2,
             n_univ = n_univ * n)
  }
  players %>%
      group_by(pos1, score1, pos2, score2) %>%
      summarise(n_univ = sum(n_univ), .groups = "drop")
}

# Sample input
players <- tibble(pos1 = 4, score1 = 0, pos2 = 8, score2 = 0, n_univ = 1)
# After two turns
players %>% roll_dirac(player = 1) %>% roll_dirac(player = 2)

# A tibble: 49 × 5
    pos1 score1  pos2 score2 n_univ
   <dbl>  <dbl> <dbl>  <dbl>  <dbl>
 1     1      1     1      1      6
 2     1      1     2      2     18
 3     1      1     3      3     36
 4     1      1     4      4     42
 5     1      1     5      5     36
 6     1      1     6      6     18
 7     1      1     7      7      6
 8     2      2     1      1      3
 9     2      2     2      2      9
10     2      2     3      3     18
# … with 39 more rows
# ℹ Use `print(n = ...)` to see more rows

After each roll, the number of universes (n_univ) is updated for each state.

Then a function to find the winners in each universe. The loop works by removing winning states (winner_universes) from the active states (players) until none remain:

find_winners <- function(players) {
  turn <- 0
  # Empty tibble to compile winners
  winner_universes <- players %>% filter(FALSE)
  
  while (nrow(players) > 0) {
    turn <- turn + 1
    
    players <- roll_dirac(players,
                          player = ifelse(turn %% 2 == 1, 1, 2))
    
    winners <- (players$score1 > 20) | (players$score2 > 20)
    if (any(winners)) {
      winner_universes <- winner_universes %>%
        bind_rows(players %>% filter(winners))
      
      players <- players %>% filter(!winners)
    }
  }
  winner_universes
}

winner_universes <- find_winners(players)

winner_universes %>%
  mutate(winner = ifelse(score1 > 20, "Player 1", "Player 2")) %>%
  group_by(winner) %>%
  summarise(n_univ = sum(n_univ), .groups = "drop") %>%
  mutate(n_univ = format(n_univ, scientific = FALSE))

# A tibble: 2 × 2
  winner   n_univ         
  <chr>    <chr>          
1 Player 1 444356092776315
2 Player 2 341960390180808

Now apply it to my input to find the puzzle answer:

players <- tibble(pos1 = player1, score1 = 0, pos2 = player2, score2 = 0,
                  n_univ = 1)
winner_universes <- find_winners(players)

winner_universes %>%
  mutate(winner = ifelse(score1 > 20, "Player 1", "Player 2")) %>%
  group_by(winner) %>%
  summarise(n_univ = sum(n_univ), .groups = "drop") %>%
  mutate(n_univ = format(n_univ, scientific = FALSE))

# A tibble: 2 × 2
  winner   n_univ         
  <chr>    <chr>          
1 Player 1 346642902541848
2 Player 2 262939886779945

Python with numpy and pandas:

from itertools import product
roll_perm = list(product([1, 2, 3], [1, 2, 3], [1, 2, 3]))
roll_perm = [sum(rolls) for rolls in roll_perm]
roll_perm = pd.DataFrame(roll_perm, columns = ['roll']) \
  .value_counts().to_frame('n').reset_index()
  
def roll_dirac(players, player = 1):
  if player == 1:
    players = players.merge(roll_perm, how = 'outer', on = 'join_key')
    players = players \
      .assign(pos1 = (players['pos1'] + players['roll'] - 1) % 10 + 1)
    players = players \
      .assign(score1 = players['score1'] + players['pos1'],
              n_univ = players['n_univ'] * players['n'])
  else:
    players = players.merge(roll_perm, how = 'outer', on = 'join_key')
    players = players \
      .assign(pos2 = (players['pos2'] + players['roll'] - 1) % 10 + 1)
    players = players \
      .assign(score2 = players['score2'] + players['pos2'],
              n_univ = players['n_univ'] * players['n'])
    
  players = players \
    .groupby(['pos1', 'score1', 'pos2', 'score2', 'join_key']) \
    .agg({'n_univ': 'sum'}).reset_index()
  return players

def find_winners(players):
  turn = 0
  winner_universes = players.drop(players.index)
  
  while len(players) > 0:
    turn += 1
    
    player = 1 if (turn % 2 == 1) else 2
    players = roll_dirac(players, player)
    
    winners = (players['score1'].values > 20) | (players['score2'].values > 20)
    if any(winners):
      winner_universes = pd.concat([winner_universes, players.loc[winners]])
      players = players.loc[~winners]
  
  return winner_universes

players = pd.DataFrame({'pos1': player1, 'pos2': player2,
                        'score1': 0, 'score2': 0, 'n_univ': 1}, index = [0])
  
# I'm not aware of a pandas function similar to tidyr::crossing, so use a hacky
#  join_key column
roll_perm['join_key'] = 0
players['join_key'] = 0

winner_universes = find_winners(players)

winner_universes \
  .assign(winner = np.where(winner_universes['score1'] > 20,
                            'Player 1', 'Player 2')) \
  .groupby(['winner']) \
  .agg({'n_univ': 'sum'})

                   n_univ
winner                   
Player 1  346642902541848
Player 2  262939886779945

Day 22: Reactor Reboot

day22 <- read_lines("day22-input.txt")
day22 %>% head()

[1] "on x=-45..0,y=-44..9,z=-39..10"   "on x=-22..26,y=-21..25,z=-2..43" 
[3] "on x=-17..35,y=-35..15,z=-27..25" "on x=-10..38,y=-46..6,z=-19..31" 
[5] "on x=-19..28,y=-48..4,z=-47..4"   "on x=-12..41,y=-45..7,z=-47..1"

Part 1

Operating at these extreme ocean depths has overloaded the submarine’s reactor; it needs to be rebooted.

The reactor core is made up of a large 3-dimensional grid made up entirely of cubes, one cube per integer 3-dimensional coordinate (x,y,z). Each cube can be either on or off; at the start of the reboot process, they are all off. (Could it be an old model of a reactor you’ve seen before?)

To reboot the reactor, you just need to set all of the cubes to either on or off by following a list of reboot steps (your puzzle input). Each step specifies a cuboid (the set of all cubes that have coordinates which fall within ranges for x, y, and z) and whether to turn all of the cubes in that cuboid on or off.

The initialization procedure only uses cubes that have x, y, and z positions of at least -50 and at most 50. For now, ignore cubes outside this region.

Execute the reboot steps. Afterward, considering only cubes in the region x=-50..50,y=-50..50,z=-50..50, how many cubes are on?

Parse the reboot steps:

reboot_steps <- tibble(x = day22) %>%
  extract(
    col = x, into = c("on", "xmin", "xmax", "ymin", "ymax", "zmin", "zmax"),
    regex = "(.*) x=(.*)\\.\\.(.*),y=(.*)\\.\\.(.*),z=(.*)\\.\\.(.*)",
    convert = TRUE
  ) %>%
  # Use a logical to indicate on/off
  mutate(on = on == "on", step_num = row_number())
reboot_steps

# A tibble: 420 × 8
   on     xmin  xmax  ymin  ymax  zmin  zmax step_num
   <lgl> <int> <int> <int> <int> <int> <int>    <int>
 1 TRUE    -45     0   -44     9   -39    10        1
 2 TRUE    -22    26   -21    25    -2    43        2
 3 TRUE    -17    35   -35    15   -27    25        3
 4 TRUE    -10    38   -46     6   -19    31        4
 5 TRUE    -19    28   -48     4   -47     4        5
 6 TRUE    -12    41   -45     7   -47     1        6
 7 TRUE    -31    15   -49    -1   -18    30        7
 8 TRUE    -15    32   -36    12   -12    33        8
 9 TRUE    -47     2   -35    12    -9    37        9
10 TRUE     -8    39   -41    10    -1    45       10
# … with 410 more rows
# ℹ Use `print(n = ...)` to see more rows

For part 1, I only need the steps within -50 and +50 in each dimension:

reboot_steps_part1 <- reboot_steps %>%
  filter(xmax >= -50, ymax >= -50, zmax >= -50,
         xmin <= 50, ymin <= 50, zmin <= 50)

Represent the 100x100x100 grid of cubes with an array and a function to update it from a single step:

cubes <- array(FALSE, dim = c(100, 100, 100))

# For my own convenience, add 50 to each range so that I can index the array
#  with 1-100
reboot_steps_part1 <- reboot_steps_part1 %>%
  mutate(across(xmin:zmax, ~ . + 50))

switch_cubes <- function(cubes, reboot_step) {
  cubes[reboot_step$xmin:reboot_step$xmax,
        reboot_step$ymin:reboot_step$ymax,
        reboot_step$zmin:reboot_step$zmax] <- reboot_step$on
  return(cubes)
}

Now apply it and take the sum to get the number of on cubes:

for (reboot_step in reboot_steps_part1 %>% split(.$step_num)) {
  cubes <- switch_cubes(cubes, reboot_step)
}
sum(cubes)

[1] 543306

Part 2

Now that the initialization procedure is complete, you can reboot the reactor.

Starting again with all cubes off, execute all reboot steps. Afterward, considering all cubes, how many cubes are on?

My solution to part 1 won’t do here.

reboot_steps %>%
  summarise(across(c(xmin, ymin, zmin), min),
            across(c(xmax, ymax, zmax), max))

# A tibble: 1 × 6
    xmin   ymin   zmin  xmax  ymax  zmax
   <int>  <int>  <int> <int> <int> <int>
1 -97543 -97547 -94763 95984 97644 96256

Can’t really work with a 20k x 20k x 20k grid in R.

Instead, for the cuboid defined in each step, I will consider every cuboid that came before it. If I find any intersecting cuboids, I will separate them into smaller cuboids that don’t intersect. For the on/off instruction of each cuboid, I will keep the last instruction.

get_cuboids <- function(reboot_steps) {
  cuboids <- tibble(xmin = numeric(), xmax = numeric(),
                    ymin = numeric(), ymax = numeric(),
                    zmin = numeric(), zmax = numeric())
  
  n_steps <- nrow(reboot_steps)
  for (cuboid1 in reboot_steps %>% split(.$step_num)) {
    message(paste0("Step ", cuboid1$step_num, " of ", n_steps))
    
    # After a lot of trial and error with the example input, I found out that I
    #  had an off-by-one error that was fixed by nudging the upper bounds
    cuboid1 <- cuboid1 %>%
      mutate(xmax = xmax + 1, ymax = ymax + 1, zmax = zmax + 1)
    
    # Declare an empty tibble to compile new cuboids
    new_cuboids <- cuboids %>% filter(FALSE)
    # Loop over the cuboids gathered so far
    for (i in seq_len(nrow(cuboids))) {
      cuboid2 <- cuboids %>% slice(i)
      
      # Check if the new cuboid overlaps with the old cuboid
      x_overlap <- (cuboid1$xmax > cuboid2$xmin) & (cuboid1$xmin < cuboid2$xmax)
      y_overlap <- (cuboid1$ymax > cuboid2$ymin) & (cuboid1$ymin < cuboid2$ymax)
      z_overlap <- (cuboid1$zmax > cuboid2$zmin) & (cuboid1$zmin < cuboid2$zmax)
      
      if (x_overlap & y_overlap & z_overlap) {
        # If the left edge of cuboid2 is to the left of cuboid1
        if (cuboid2$xmin < cuboid1$xmin) {
          # Slice off that portion into a new cuboid
          new_cuboids <- new_cuboids %>%
            bind_rows(cuboid2 %>% mutate(xmax = cuboid1$xmin))
          # And shrink cuboid2, as the new cuboid covers that area already
          cuboid2 <- cuboid2 %>% mutate(xmin = cuboid1$xmin)
        }
        # Do the same for the other 5 directions
        if (cuboid2$xmax > cuboid1$xmax) {
          new_cuboids <- new_cuboids %>%
            bind_rows(cuboid2 %>% mutate(xmin = cuboid1$xmax))
          cuboid2 <- cuboid2 %>% mutate(xmax = cuboid1$xmax)
        }
        if (cuboid2$ymin < cuboid1$ymin) {
          new_cuboids <- new_cuboids %>%
            bind_rows(cuboid2 %>% mutate(ymax = cuboid1$ymin))
          cuboid2 <- cuboid2 %>% mutate(ymin = cuboid1$ymin)
        }
        if (cuboid2$ymax > cuboid1$ymax) {
          new_cuboids <- new_cuboids %>%
            bind_rows(cuboid2 %>% mutate(ymin = cuboid1$ymax))
          cuboid2 <- cuboid2 %>% mutate(ymax = cuboid1$ymax)
        }
        if (cuboid2$zmin < cuboid1$zmin) {
          new_cuboids <- new_cuboids %>%
            bind_rows(cuboid2 %>% mutate(zmax = cuboid1$zmin))
          cuboid2 <- cuboid2 %>% mutate(zmin = cuboid1$zmin)
        }
        if (cuboid2$zmax > cuboid1$zmax) {
          new_cuboids <- new_cuboids %>%
            bind_rows(cuboid2 %>% mutate(zmin = cuboid1$zmax))
          cuboid2 <- cuboid2 %>% mutate(zmax = cuboid1$zmax)
        }
      }
      else {
        new_cuboids <- new_cuboids %>% bind_rows(cuboid2)
      }
    }
    new_cuboids <- new_cuboids %>% bind_rows(cuboid1)
    cuboids <- new_cuboids
  }
  return(cuboids)
}

As a demonstration, consider the first 3 steps (which happen to have overlapping cuboids) in just 2 dimensions:

reboot_steps3 <- reboot_steps %>% slice(1:3)

p <- reboot_steps3 %>%
  mutate(step_num = factor(step_num)) %>%
  ggplot(aes(xmin = xmin, xmax = xmax, ymin = ymin, ymax = ymax)) +
  geom_rect(aes(fill = step_num),alpha = 0.5)
p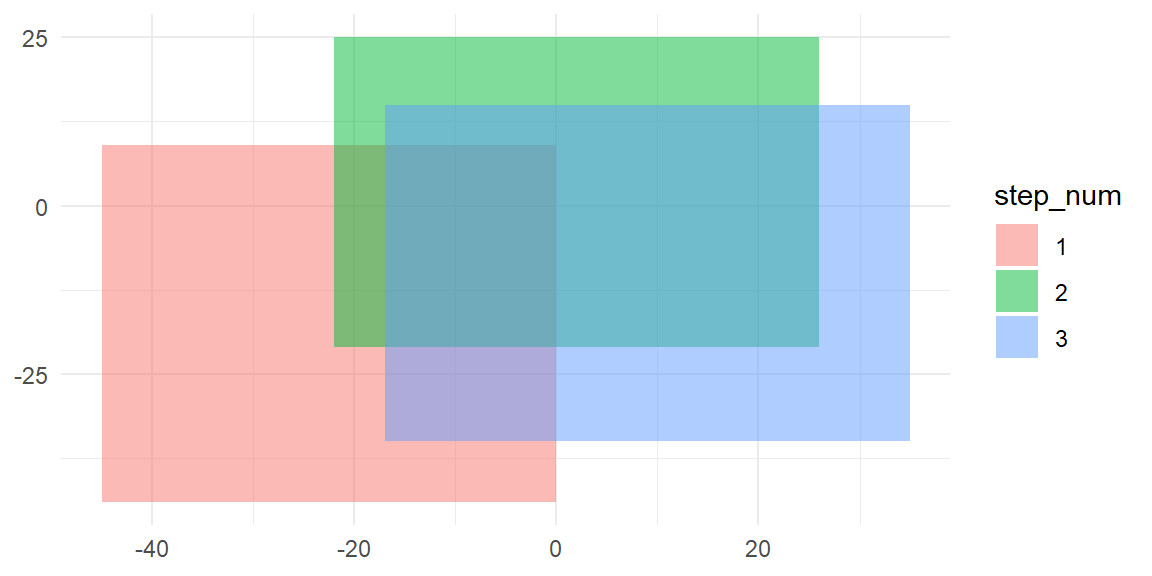

These are the resulting cuboids after splitting them at the intersections:

p +
  geom_rect(
    data = get_cuboids(reboot_steps3) %>%
      # Shrink the areas slightly to visualize the borders
      mutate(across(c(xmin, ymin), ~ .x + 0.5),
             across(c(xmax, ymax), ~ .x - 0.5)),
    fill = NA, color = "black")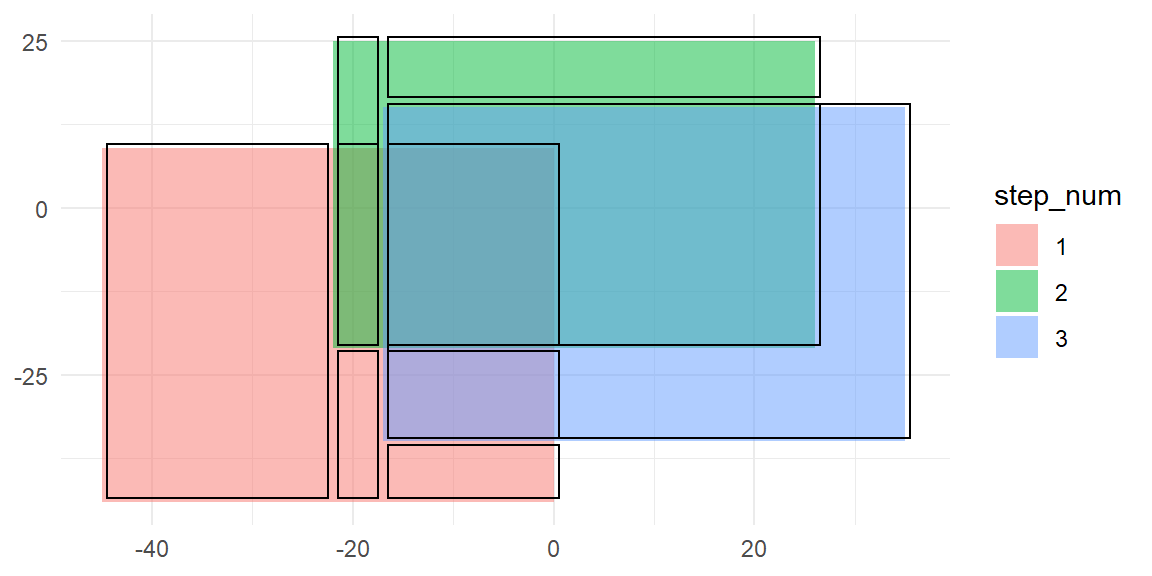

Now run it on the full input (and time it because I expect it to take a long time):

tic()
cubes <- get_cuboids(reboot_steps)
toc()

1062.81 sec elapsed

~17 minute run time.

Now I have a list of cuboids which are non-overlapping. I can filter down to just the ones that are on and count their volumes to get the total number of on cubes:

cubes %>%
  filter(on) %>%
  mutate(volume = (xmax - xmin) * (ymax - ymin) * (zmax - zmin)) %>%
  summarise(n_on = sum(volume) %>% format(scientific = FALSE))

# A tibble: 1 × 1
  n_on            
  <chr>           
1 1285501151402480

Day 23: Amphipod

day23 <- read_lines("day23-input.txt")
day23 %>% str_c(collapse = "\n") %>% message()

#############
#...........#
###A#D#A#B###
  #C#C#D#B#
  #########

Part 1

A group of amphipods notice your fancy submarine and flag you down. “With such an impressive shell,” one amphipod says, “surely you can help us with a question that has stumped our best scientists.”

They go on to explain that a group of timid, stubborn amphipods live in a nearby burrow. Four types of amphipods live there: Amber (A), Bronze (B), Copper (C), and Desert (D). They live in a burrow that consists of a hallway and four side rooms. The side rooms are initially full of amphipods, and the hallway is initially empty.

They give you a diagram of the situation (your puzzle input), including locations of each amphipod (A, B, C, or D, each of which is occupying an otherwise open space), walls (#), and open space (.).

For example:

#############
#...........#
###B#C#B#D###
  #A#D#C#A#
  #########`

The amphipods would like a method to organize every amphipod into side rooms so that each side room contains one type of amphipod and the types are sorted A-D going left to right, like this:

#############
#...........#
###A#B#C#D###
  #A#B#C#D#
  #########

Amphipods can move up, down, left, or right so long as they are moving into an unoccupied open space. Each type of amphipod requires a different amount of energy to move one step: Amber amphipods require 1 energy per step, Bronze amphipods require 10 energy, Copper amphipods require 100, and Desert ones require 1000. The amphipods would like you to find a way to organize the amphipods that requires the least total energy.

However, because they are timid and stubborn, the amphipods have some extra rules:

Amphipods will never stop on the space immediately outside any room. They can move into that space so long as they immediately continue moving. (Specifically, this refers to the four open spaces in the hallway that are directly above an amphipod starting position.)

Amphipods will never move from the hallway into a room unless that room is their destination room and that room contains no amphipods which do not also have that room as their own destination. If an amphipod’s starting room is not its destination room, it can stay in that room until it leaves the room. (For example, an Amber amphipod will not move from the hallway into the right three rooms, and will only move into the leftmost room if that room is empty or if it only contains other Amber amphipods.)

Once an amphipod stops moving in the hallway, it will stay in that spot until it can move into a room. (That is, once any amphipod starts moving, any other amphipods currently in the hallway are locked in place and will not move again until they can move fully into a room.)

What is the least energy required to organize the amphipods?

I’ve been slacking a bit on my Python, so I’ll attempt this one in Python first (and if I have time, reproduce the solution in R). Parse the data into a list of lists:

letters = [[c for c in line if c.isalpha()] for line in r.day23[2:4]]
letters

[['A', 'D', 'A', 'B'], ['C', 'C', 'D', 'B']]

The first element is the top row of each room, and the second is the bottom. Now represent the initial state of the amphipod locations with a tuple of the hallway (starting empty) and the rooms:

rooms = [(letter1, letter2) for letter1, letter2 in zip(*letters)]
# Represent the empty hallway with 11 None values
hallway = (None, ) * 11
initial_state = (hallway, *rooms)
initial_state

((None, None, None, None, None, None, None, None, None, None, None), ('A', 'C'), ('D', 'C'), ('A', 'D'), ('B', 'B'))

Define the target state – A, B, C and D in the rooms in order left to right:

target_state = ((None, ) * 11, ('A', 'A'), ('B', 'B'), ('C', 'C'), ('D', 'D'))

Also define some helpful dict mappings that define connections between rooms, halls, amphipods and their energy costs to move:

# The rooms targeted by each amphipod
target_rooms = {'A': 1, 'B': 2, 'C': 3, 'D': 4}
# This dict maps rooms (numeric 1 = A, 2 = B, etc) to numeric locations in the
#  hallway, e.g. room B leads to hallway location 4
room_to_hall = {1: 2, 2: 4, 3: 6, 4: 8}
energy_costs = {'A': 1, 'B': 10, 'C': 100, 'D': 1000}

Define the workhorse function of the problem, which loops over all amphipods and returns possible states and their energy costs:

def get_possible_moves(state):
  # For each room, consider moving the top-most amphipods
  for i in range(1, 5):
    # Look for the first non-empty space
    if state[i][0] is not None:
      # The top spot is occupied
      top_loc = 0
    elif state[i][1] is not None:
      # The bottom spot is occupied 
      top_loc = 1
    else:
      # Otherwise, nothing in this room so continue
      continue
    
    # In order to mutate the tuple state, need to convert to list of lists
    state_list = list(map(list, state))
    # The amphipod letter at the top of the room
    letter = state_list[i][top_loc]
    
    # If this letter is in the right room, and everything below it is as well
    if target_rooms[letter] == i and \
        all(letter == letter_below for letter_below in state[i][top_loc:]):
      continue # Don't move it
          
    # Move it
    steps = top_loc 
    state_list[i][top_loc] = None
    
    # Find spaces in the hallway that it could possibly move
    possible_locs = []
    # Look to the left of the room first
    for j in range(room_to_hall[i]):
      # If not in front of the door
      if j not in [2, 4, 6, 8]:
        possible_locs.append(j)
      # If that space in the hallway is occupied, it is not possible to move
      if state_list[0][j] is not None:
        possible_locs.clear()
    # Look to the right of the room second
    for j in range(room_to_hall[i], 11):
      if state_list[0][j] is not None:
        break
      if j not in [2, 4, 6, 8]:
        possible_locs.append(j)
    
    # The new states will have unique hallways, as a letter moves from a room
    new_state = list(map(tuple, state_list))
    hallway = state[0]
    
    for loc in possible_locs:
      hallway_list = list(hallway)
      hallway_list[loc] = letter
      new_state[0] = tuple(hallway_list)
      # Count the number of steps to get to this space, and multiply by energy
      energy = (steps + 1 + abs(loc - room_to_hall[i])) * energy_costs[letter]
      yield tuple(new_state), energy
      
  # For each amphipod in the hallway, consider moving into rooms
  for i,letter in enumerate(state[0]):
    if letter is None: continue
    
    # Find the target room for this letter
    target_room = target_rooms[letter]
    # And its current occupants
    room_letters = set(state[target_room]).discard(None)
    # And the hallway location right outside
    target_hallway = room_to_hall[target_room]
    # If the room has other letters in it, don't both moving into it
    if room_letters and {letter} != room_letters:
      continue
    
    # If to the left of the target location
    if i < target_hallway:
      # Consider all locations to the left
      hall_locs = slice(i + 1, target_hallway + 1)
    else:
      # Otherwise, all locations to the right
      hall_locs = slice(target_hallway, i)
    
    # If there is an amphipod in the way, break
    for loc in state[0][hall_locs]:
      if loc is not None:
        break
    else:
      steps = abs(i - target_hallway)
      state_list = list(map(list, state))
      # Remove it from the hall
      state_list[0][i] = None
      # Get the list of current room occupants
      room_list = state_list[target_room]
      
      # Consider all locations in the room
      for room_loc, other_letter in reversed(list(enumerate(room_list))):
        if other_letter is None: break
      
      # If the top location is empty (as expected) move the amphipod there
      assert room_list[room_loc] is None
      room_list[room_loc] = letter
      steps += room_loc + 1
      
      energy = steps * energy_costs[letter]
      yield tuple(map(tuple, state_list)), steps * energy

Now to define a function that repeatedly looks for new states until it finds the target state. To drastically reduce computation time, I will take advantage of memoization from the functools package. This works by caching the results of a function for specific inputs (here the state), and returning the cached result instead of re-computing it.

from functools import cache

@cache
def steps_to_target(state):
  if state == target_state: return 0
  
  possible_costs = []
  
  for new_state, energy in get_possible_moves(state):
    possible_costs.append(energy + steps_to_target(new_state))
    
  return min(possible_costs)

steps_to_target(initial_state)

Error in py_call_impl(callable, dots$args, dots$keywords): RecursionError: maximum recursion depth exceeded in comparison

Even with memoization, this requires me to adjust the recursion depth:

import sys
print(sys.getrecursionlimit())

sys.setrecursionlimit(30000)

steps_to_target(initial_state)

Unfortunately, I can’t get this working in the RStudio IDE with reticulate – the R session immediately crashes. I ran it outside of RStudio and found that the least energy required to reach the target state was 13495.

Part 2

As you prepare to give the amphipods your solution, you notice that the diagram they handed you was actually folded up. As you unfold it, you discover an extra part of the diagram.

Between the first and second lines of text that contain amphipod starting positions, insert the following lines:

  #D#C#B#A#
  #D#B#A#C#

So, the above example now becomes:

#############
#...........#
###B#C#B#D###
  #D#C#B#A#
  #D#B#A#C#
  #A#D#C#A#
  #########

The amphipods still want to be organized into rooms similar to before:

#############
#...........#
###A#B#C#D###
  #A#B#C#D#
  #A#B#C#D#
  #A#B#C#D#
  #########

Using the initial configuration from the full diagram, what is the least energy required to organize the amphipods?

Thankfully I predicted the rooms getting bigger in part 2, so I only have to add a couple lines of code to the get_possible_moves function:

def get_possible_moves(state):
  for i in range(1, 5):
    if state[i][0] is not None:
      top_loc = 0
    elif state[i][1] is not None:
      top_loc = 1
    elif state[i][2] is not None:
      top_loc = 2
    elif state[i][3] is not None:
      top_loc = 3
    else:
      # Otherwise, nothing in this room so continue
      continue
  # Rest of the function remains the same
  # ...

The answer to this part is 53767 energy.

Day 24: Arithmetic Logic Unit

day24 <- read_lines("day24-input.txt")
head(day24)

[1] "inp w"    "mul x 0"  "add x z"  "mod x 26" "div z 1"  "add x 10"

Part 1

Very long puzzle statement

Magic smoke starts leaking from the submarine’s arithmetic logic unit (ALU). Without the ability to perform basic arithmetic and logic functions, the submarine can’t produce cool patterns with its Christmas lights!

It also can’t navigate. Or run the oxygen system.

Don’t worry, though - you probably have enough oxygen left to give you enough time to build a new ALU.

The ALU is a four-dimensional processing unit: it has integer variables w, x, y, and z. These variables all start with the value 0. The ALU also supports six instructions:

inp a - Read an input value and write it to variable a.

add a b - Add the value of a to the value of b, then store the result in variable a.

mul a b - Multiply the value of a by the value of b, then store the result in variable a.

div a b - Divide the value of a by the value of b, truncate the result to an integer, then store the result in variable a. (Here, “truncate” means to round the value toward zero.)

mod a b - Divide the value of a by the value of b, then store the remainder in variable a. (This is also called the modulo operation.)

eql a b - If the value of a and b are equal, then store the value 1 in variable a. Otherwise, store the value 0 in variable a.

In all of these instructions, a and b are placeholders; a will always be the variable where the result of the operation is stored (one of w, x, y, or z), while b can be either a variable or a number. Numbers can be positive or negative, but will always be integers.

The ALU has no jump instructions; in an ALU program, every instruction is run exactly once in order from top to bottom. The program halts after the last instruction has finished executing.

(Program authors should be especially cautious; attempting to execute div with b=0 or attempting to execute mod with a<0 or b<=0 will cause the program to crash and might even damage the ALU. These operations are never intended in any serious ALU program.)

Once you have built a replacement ALU, you can install it in the submarine, which will immediately resume what it was doing when the ALU failed: validating the submarine’s model number. To do this, the ALU will run the MOdel Number Automatic Detector program (MONAD, your puzzle input).

Submarine model numbers are always fourteen-digit numbers consisting only of digits 1 through 9. The digit 0 cannot appear in a model number.

When MONAD checks a hypothetical fourteen-digit model number, it uses fourteen separate inp instructions, each expecting a single digit of the model number in order of most to least significant. (So, to check the model number 13579246899999, you would give 1 to the first inp instruction, 3 to the second inp instruction, 5 to the third inp instruction, and so on.) This means that when operating MONAD, each input instruction should only ever be given an integer value of at least 1 and at most 9.

Then, after MONAD has finished running all of its instructions, it will indicate that the model number was valid by leaving a 0 in variable z. However, if the model number was invalid, it will leave some other non-zero value in z.

MONAD imposes additional, mysterious restrictions on model numbers, and legend says the last copy of the MONAD documentation was eaten by a tanuki. You’ll need to figure out what MONAD does some other way.

To enable as many submarine features as possible, find the largest valid fourteen-digit model number that contains no 0 digits. What is the largest model number accepted by MONAD?

These are some very confusing instructions. My TLDR is that the puzzle input is the code, through which I run many different 14 digit model numbers, and find the largest valid number (that contains no 0 digits). Parse the MONAD instruction list:

monad <- tibble(x = day24) %>%
  mutate(step_num = row_number()) %>%
  separate(x, into = c("operation", "var1", "var2"), sep = " ", fill = "right")
monad

# A tibble: 252 × 4
   operation var1  var2  step_num
   <chr>     <chr> <chr>    <int>
 1 inp       w     <NA>         1
 2 mul       x     0            2
 3 add       x     z            3
 4 mod       x     26           4
 5 div       z     1            5
 6 add       x     10           6
 7 eql       x     w            7
 8 eql       x     0            8
 9 mul       y     0            9
10 add       y     25          10
# … with 242 more rows
# ℹ Use `print(n = ...)` to see more rows

252 steps in the program. How many input operations are there?

monad %>% count(operation)

# A tibble: 6 × 2
  operation     n
  <chr>     <int>
1 add          98
2 div          14
3 eql          28
4 inp          14
5 mod          14
6 mul          84

14 inputs (inp) for the 14 digit model number. So I need make a function which takes any 14 digit model number (that doesn’t contain 0), and will be considered valid if the z variable is non-zero.

check_model_number <- function(model_number) {
  model_number <- strsplit(model_number, "")[[1]]
  
  # Place the model number into the input instructions
  monad$var2[is.na(monad$var2)] <- model_number
  
  reduce(monad %>% split(.$step_num), run_monad_instruction,
         .init = list(w = 0, x = 0, y = 0, z = 0))
}

run_monad_instruction <- function(vars, instr) {
  # Variable 2 is either a number
  if (!is.na(as.numeric(instr$var2))) {
    var2 <- as.numeric(instr$var2)
  # Or variable which has a number assigned
  } else {
    var2 <- as.numeric(vars[[instr$var2]])
  }
  
  switch(instr$operation,
    "inp" = {
      vars[[instr$var1]] <- var2
    },
    "add" = {
      vars[[instr$var1]] <- vars[[instr$var1]] + var2
    },
    "mul" = {
      vars[[instr$var1]] <- vars[[instr$var1]] * var2
    },
    "div" = {
      stopifnot(var2 != 0)
      vars[[instr$var1]] <- trunc(vars[[instr$var1]] / var2)
    },
    "mod" = {
      stopifnot(vars[[instr$var1]] >= 0)
      stopifnot(var2 > 0)
      vars[[instr$var1]] <- vars[[instr$var1]] %% var2
    },
    "eql" = {
      vars[[instr$var1]] <- ifelse(vars[[instr$var1]] == var2, 1, 0)
    }
  )
  return(vars)
}

Now I can check any 14 digit number, like the example input 13579246899999:

check_model_number("13579246899999")

$w
[1] 9

$x
[1] 1

$y
[1] 20

$z
[1] 134689198

This number returns a non-zero z, and so is invalid.

The problem now is: how to check so many model numbers? I could start from 99999999999999 and decrease by 1 until I find a valid number.

check_model_number("99999999999999")

$w
[1] 9

$x
[1] 1

$y
[1] 20

$z
[1] 8937728

But with 9^14 = 22,876,792,454,961 possible numbers to check, the brute force approach would not finish in any reasonable time frame. There has to be a simpler way to approach the problem. Looking at the raw input, there is definitely a pattern to the instructions. The input instructions come at regular intervals (1st, 19th, 37th, 55th, …). Split the monad by the input instructions, and compare instructions side-by-side:

day24 %>%
  split(cumsum(str_detect(., "inp"))) %>%
  map_dfc(as_tibble) %>%
  rename_with(~str_replace(., "value...", "input ")) %>%
  mutate(step_num = row_number()) %>%
  gt(rowname_col = "step_num")

	input 1	input 2	input 3	input 4	input 5	input 6	input 7	input 8	input 9	input 10	input 11	input 12	input 13	input 14
1	inp w	inp w	inp w	inp w	inp w	inp w	inp w	inp w	inp w	inp w	inp w	inp w	inp w	inp w
2	mul x 0	mul x 0	mul x 0	mul x 0	mul x 0	mul x 0	mul x 0	mul x 0	mul x 0	mul x 0	mul x 0	mul x 0	mul x 0	mul x 0
3	add x z	add x z	add x z	add x z	add x z	add x z	add x z	add x z	add x z	add x z	add x z	add x z	add x z	add x z
4	mod x 26	mod x 26	mod x 26	mod x 26	mod x 26	mod x 26	mod x 26	mod x 26	mod x 26	mod x 26	mod x 26	mod x 26	mod x 26	mod x 26
5	div z 1	div z 1	div z 1	div z 26	div z 1	div z 26	div z 1	div z 26	div z 1	div z 1	div z 26	div z 26	div z 26	div z 26
6	add x 10	add x 13	add x 15	add x -12	add x 14	add x -2	add x 13	add x -12	add x 15	add x 11	add x -3	add x -13	add x -12	add x -13
7	eql x w	eql x w	eql x w	eql x w	eql x w	eql x w	eql x w	eql x w	eql x w	eql x w	eql x w	eql x w	eql x w	eql x w
8	eql x 0	eql x 0	eql x 0	eql x 0	eql x 0	eql x 0	eql x 0	eql x 0	eql x 0	eql x 0	eql x 0	eql x 0	eql x 0	eql x 0
9	mul y 0	mul y 0	mul y 0	mul y 0	mul y 0	mul y 0	mul y 0	mul y 0	mul y 0	mul y 0	mul y 0	mul y 0	mul y 0	mul y 0
10	add y 25	add y 25	add y 25	add y 25	add y 25	add y 25	add y 25	add y 25	add y 25	add y 25	add y 25	add y 25	add y 25	add y 25
11	mul y x	mul y x	mul y x	mul y x	mul y x	mul y x	mul y x	mul y x	mul y x	mul y x	mul y x	mul y x	mul y x	mul y x
12	add y 1	add y 1	add y 1	add y 1	add y 1	add y 1	add y 1	add y 1	add y 1	add y 1	add y 1	add y 1	add y 1	add y 1
13	mul z y	mul z y	mul z y	mul z y	mul z y	mul z y	mul z y	mul z y	mul z y	mul z y	mul z y	mul z y	mul z y	mul z y
14	mul y 0	mul y 0	mul y 0	mul y 0	mul y 0	mul y 0	mul y 0	mul y 0	mul y 0	mul y 0	mul y 0	mul y 0	mul y 0	mul y 0
15	add y w	add y w	add y w	add y w	add y w	add y w	add y w	add y w	add y w	add y w	add y w	add y w	add y w	add y w
16	add y 10	add y 5	add y 12	add y 12	add y 6	add y 4	add y 15	add y 3	add y 7	add y 11	add y 2	add y 12	add y 4	add y 11
17	mul y x	mul y x	mul y x	mul y x	mul y x	mul y x	mul y x	mul y x	mul y x	mul y x	mul y x	mul y x	mul y x	mul y x
18	add z y	add z y	add z y	add z y	add z y	add z y	add z y	add z y	add z y	add z y	add z y	add z y	add z y	add z y

The only steps which differ from input to input are:

Step 1: inp w which will take a different digit from the model number every time
Step 5: div z 1 and div z 26
Step 6: add x 10, 13, 15, -12, 14, -2, 11, -3, -13
Step 16: add y 10, 5, 12, 6, 4, 15, 3, 7, 11, 2

So I can write a simple function which takes a few variables and runs through all the steps:

monad_simple_step <- function(z = 0, w = 1, step5 = 1, step6 = 10, step16 = 3) {
  # Step 2
  x <- 0
  # Step 3
  x <- z
  # Step 4
  x <- x %% 26
  # Step 5
  z <- trunc(z / step5)
  # Step 6
  x <- x + step6
  # Step 7
  x <- as.numeric(x == w)
  # Step 8
  x <- as.numeric(x == 0)
  # Step 9
  y <- 0
  # Step 10
  y <- y + 25
  # Step 11
  y <- y * x
  # Step 12
  y <- y + 1
  # Step 13
  z <- z * y
  # Step 14
  y <- 0
  # Step 15
  y <- y + w
  # Step 16
  y <- y + step16
  # Step 17
  y <- y * x
  # Step 18
  z <- z + y
  # Output
  z
}
monad_simple_step(w = 5)

[1] 8

monad_simple_step(z = 8, w = 3, step5 = 26, step6 = -12, step16 = 4)

[1] 7

Obviously a lot of these steps can be simplified further. A simpler function could have two lines like this:

monad_simple_step <- function(z = 0, w = 1, step5 = 1, step6 = 10, step16 = 3) {
  x <- as.numeric(((z %% 26) + step6) != w)
  trunc(z / step5) * ((25 * x) + 1) + (w + step16) * x
}
monad_simple_step(w = 5)

[1] 8

monad_simple_step(z = 8, w = 3, step5 = 26, step6 = -12, step16 = 4)

[1] 7

I can also simplify my monad input down to just the important steps:

monad_simple <- monad %>%
  mutate(input_step = cumsum(operation == "inp")) %>%
  group_by(input_step) %>%
  mutate(sub_step = row_number()) %>%
  ungroup() %>%
  filter(sub_step %in% c(5, 6, 16)) %>%
  select(input_step, sub_step, var2) %>%
  pivot_wider(names_from = sub_step, values_from = var2) %>%
  rename_with(~paste0("step", .), .cols = c(`5`, `6`, `16`)) %>%
  mutate(across(everything(), as.integer))
monad_simple

# A tibble: 14 × 4
   input_step step5 step6 step16
        <int> <int> <int>  <int>
 1          1     1    10     10
 2          2     1    13      5
 3          3     1    15     12
 4          4    26   -12     12
 5          5     1    14      6
 6          6    26    -2      4
 7          7     1    13     15
 8          8    26   -12      3
 9          9     1    15      7
10         10     1    11     11
11         11    26    -3      2
12         12    26   -13     12
13         13    26   -12      4
14         14    26   -13     11

This function will run a model number through the above steps and return the value of z:

check_model_number_simple <- function(model_number) {
  m <- monad_simple %>%
    mutate(w = as.integer(strsplit(model_number, "")[[1]]))
  
  reduce(
    transpose(m),
    function(z, args) {
      monad_simple_step(z, args$w, args$step5, args$step6, args$step16)
    },
    .init = 0
  )
}
check_model_number_simple("99999999999999")

[1] 8937728

This will run much faster than my previous check_model_number function, but doesn’t solve the main problem: it still requires checking every model number until we find z = 0. So it needs to be broken down even more.

Consider the line:

x <- as.numeric(((z %% 26) + step6) != w)

This will only ever be 0 or 1, depending on equality with the input value w (which ranges 1 to 9). Also notice that step6 and the sign of step5 are related:

monad_simple %>% count(step5, step6)

# A tibble: 9 × 3
  step5 step6     n
  <int> <int> <int>
1     1    10     1
2     1    11     1
3     1    13     2
4     1    14     1
5     1    15     2
6    26   -13     2
7    26   -12     3
8    26    -3     1
9    26    -2     1

Since w can only take values 1 to 9, any values of step6 > 9 will also lead to inequality with w and therefore x = 1. The values of step6 > 9 correspond to step5 = 1, and so x is always 1 in these cases.

The x value works sort of as an on/off binary switch that feeds into the next line:

z <- trunc(z / step5) * ((25 * x) + 1) + (w + step16) * x

Break this down into three terms:

term1 <- trunc(z / step5)
term2 <- (25 * x) + 1
term3 <- (w + step16) * x
z <- term1 * term2 + term3

If x = 0, then term2 = 1, and this term does nothing to z
If x = 0, then term3 = 0, and this term does nothing to z
If x = 1, then term2 = 26
If x = 1, then term3 = w + step16

The number 26 occurring so frequently means we should be thinking in base 26 numbers. Here is what happens to z under different conditions, and how we can think of z in base 26:

term1
- step5 = 1
  - term1 = z (no change)
- step5 = 26
  - term1 = z / 26 (remove an order)
term2
- = 1 (no change)
- = 26 (add an order)
term3
- = 0 no change)
- = w + step16 (add to the number)

I’m not very familiar with these terms as a non-CS grad, but apparently this mimics a stack data structure which can push a value (adds it to the stack) or pop the most recent (remove from the stack).

If step5 = 1, then term3 is pushing the value of w + step16 onto the stack (which will be less than 26 for the possible values of w and step16). Otherwise step5 = 26, which pops the last value from the stack. To get a valid model number, we need z = 0, so all digits need to be popped off the stack. There are 7 each of step5 = 1 and 26 so we can equally push and pop the digits until the stack is empty.

This means that the lines with step5 = 26, x = as.numeric(((z %% 26) + step6) != w) must be 0, which requires that the pushed digit w + step16 from the previous step be equal to the next step’s w - step6.

My specific input corresponds to the following push and pop operations on the 14 digits of a model number:

monad_simple %>%
  transmute(
    input_step,
    push_pop = ifelse(step5 == 1, "push", "pop"),
    step6, step16,
    operation = ifelse(
      push_pop == "push",
      glue::glue("push model_num[{input_step}] + {step16}"),
      glue::glue("pop requires model_num[{input_step}] = popped_val {step6}")
    )
  ) %>%
  gt()

input_step	push_pop	step6	step16	operation
1	push	10	10	push model_num[1] + 10
2	push	13	5	push model_num[2] + 5
3	push	15	12	push model_num[3] + 12
4	pop	-12	12	pop requires model_num[4] = popped_val -12
5	push	14	6	push model_num[5] + 6
6	pop	-2	4	pop requires model_num[6] = popped_val -2
7	push	13	15	push model_num[7] + 15
8	pop	-12	3	pop requires model_num[8] = popped_val -12
9	push	15	7	push model_num[9] + 7
10	push	11	11	push model_num[10] + 11
11	pop	-3	2	pop requires model_num[11] = popped_val -3
12	pop	-13	12	pop requires model_num[12] = popped_val -13
13	pop	-12	4	pop requires model_num[13] = popped_val -12
14	pop	-13	11	pop requires model_num[14] = popped_val -13

So the model number requirements unique to my MONAD are:

model_num[4] = model_num[3] - 12 + 12
model_num[6] = model_num[5] - 2 + 6
model_num[8] = model_num[7] - 12 + 15
model_num[11] = model_num[10] - 3 + 11
model_num[12] = model_num[9] - 13 + 7
model_num[13] = model_num[2] - 12 + 5
model_num[14] = model_num[1] - 13 + 10

Then finding the maximum valid model number doesn’t require any programming, just some basic logic and picking the max possible value for each digit in order:

model_num[1] = 9
- model_num[14] = 9 - 3 = 6
model_num[2] = 9
- model_num[13] = 9 - 7 = 2
model_num[3] = 9
- model_num[4] = 9
model_num[5] = 5
- model_num[6] = 5 + 4 = 9
model_num[7] = 6
- model_num[8] = 6 + 3 = 9
model_num[10] = 1
- model_num[11] = 1 + 8 = 9
model_num[9] = 9
- model_num[12] = 9 - 6 = 3

This corresponds to 99995969919326. Before submitting it, I can check that z = 0 with my functions:

check_model_number("99995969919326")

$w
[1] 6

$x
[1] 0

$y
[1] 0

$z
[1] 0

check_model_number_simple("99995969919326")

[1] 0

Part 2

As the submarine starts booting up things like the Retro Encabulator, you realize that maybe you don’t need all these submarine features after all.

What is the smallest model number accepted by MONAD?

The same rules as part 1 apply, I just need to pick the lowest digits possible:

model_num[1] = 4
- model_num[14] = 4 - 3 = 1
model_num[2] = 8
- model_num[13] = 8 - 7 = 1
model_num[3] = 1
- model_num[4] = 1
model_num[5] = 1
- model_num[6] = 1 + 4 = 5
model_num[7] = 1
- model_num[8] = 1 + 3 = 4
model_num[10] = 1
- model_num[11] = 1 + 8 = 9
model_num[9] = 7
- model_num[12] = 7 - 6 = 1

This corresponds to 48111514719111.

check_model_number("48111514719111")

$w
[1] 1

$x
[1] 0

$y
[1] 0

$z
[1] 0

check_model_number_simple("48111514719111")

[1] 0

Day 25: Sea Cucumber

day25 <- read_lines("day25-input.txt")
head(day25) %>% str_trunc(70)

[1] ".v.v.v>...>vv>v>>>.v>..v>.v.>.>v>.v.v.>>v...>.>....>.>vv>>>.....>>...."
[2] ">.v>..v.>>vv.>>v...v.>.>..v.>.>.>vvv..>>>.>...>v>.>>v....>>>>...>v...."
[3] ".vv>>...v>..v..v>v.>vvv.v.v>>.....v>>.......>...v>.v>.v.vv.v.>v>v.v..."
[4] ".>.>v.>vv.v...v.>>v>.>v..vv>..v.v.>...v....>vvvvvv>>>v..vv.v.v>>.>>..."
[5] "..>.....v.>>..>>.v>v.>.>>.>..vv.v>>.>..>.>..v>>...>.>>.vv>>>..>>>>...."
[6] "v...>..>..v>.vv.>>.>...>>....v.......v>...v.vvvvv>..v...>.v.>.>>v>v..."

Part 1

This is it: the bottom of the ocean trench, the last place the sleigh keys could be. Your submarine’s experimental antenna still isn’t boosted enough to detect the keys, but they must be here. All you need to do is reach the seafloor and find them.

At least, you’d touch down on the seafloor if you could; unfortunately, it’s completely covered by two large herds of sea cucumbers, and there isn’t an open space large enough for your submarine.

You suspect that the Elves must have done this before, because just then you discover the phone number of a deep-sea marine biologist on a handwritten note taped to the wall of the submarine’s cockpit.

“Sea cucumbers? Yeah, they’re probably hunting for food. But don’t worry, they’re predictable critters: they move in perfectly straight lines, only moving forward when there’s space to do so. They’re actually quite polite!”

You explain that you’d like to predict when you could land your submarine.

“Oh that’s easy, they’ll eventually pile up and leave enough space for– wait, did you say submarine? And the only place with that many sea cucumbers would be at the very bottom of the Mariana–” You hang up the phone.

There are two herds of sea cucumbers sharing the same region; one always moves east (>), while the other always moves south (v). Each location can contain at most one sea cucumber; the remaining locations are empty (.). The submarine helpfully generates a map of the situation (your puzzle input).

Every step, the sea cucumbers in the east-facing herd attempt to move forward one location, then the sea cucumbers in the south-facing herd attempt to move forward one location. When a herd moves forward, every sea cucumber in the herd first simultaneously considers whether there is a sea cucumber in the adjacent location it’s facing (even another sea cucumber facing the same direction), and then every sea cucumber facing an empty location simultaneously moves into that location.

Due to strong water currents in the area, sea cucumbers that move off the right edge of the map appear on the left edge, and sea cucumbers that move off the bottom edge of the map appear on the top edge. Sea cucumbers always check whether their destination location is empty before moving, even if that destination is on the opposite side of the map. To find a safe place to land your submarine, the sea cucumbers need to stop moving.

Find somewhere safe to land your submarine. What is the first step on which no sea cucumbers move?

Seems like a nice easy one to finish. Put the input into a matrix:

seafloor <- day25 %>%
  map(~strsplit(., "")[[1]]) %>%
  unlist() %>%
  matrix(nrow = length(day25), byrow = TRUE)
seafloor[1:10, 1:10]

      [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10]
 [1,] "."  "v"  "."  "v"  "."  "v"  ">"  "."  "."  "."  
 [2,] ">"  "."  "v"  ">"  "."  "."  "v"  "."  ">"  ">"  
 [3,] "."  "v"  "v"  ">"  ">"  "."  "."  "."  "v"  ">"  
 [4,] "."  ">"  "."  ">"  "v"  "."  ">"  "v"  "v"  "."  
 [5,] "."  "."  ">"  "."  "."  "."  "."  "."  "v"  "."  
 [6,] "v"  "."  "."  "."  ">"  "."  "."  ">"  "."  "."  
 [7,] "v"  ">"  "v"  ">"  "."  "v"  ">"  "."  "."  "v"  
 [8,] "."  "."  "."  "."  "."  "."  "."  "v"  "."  "."  
 [9,] "v"  ">"  "."  "v"  ">"  "."  "."  "v"  "."  "."  
[10,] "."  "v"  ">"  ">"  ">"  ">"  ">"  ">"  "v"  "."

Define functions to move sea cucumbers east or south:

max_col <- ncol(seafloor)
max_row <- nrow(seafloor)

move_east <- function(seafloor) {
  east_idx <- which(seafloor == ">", arr.ind = TRUE)
  
  seafloor_new <- seafloor
  for (i in 1:nrow(east_idx)) {
    # Find the adjacent space (one column over)
    adjacent_col <- east_idx[i, 2] + 1
    # If off the right edge of the map, back to the left
    if (adjacent_col > max_col) {
      adjacent_col <- adjacent_col - max_col
    }
    # If unoccupied, move it
    if (seafloor[east_idx[i, 1], adjacent_col] == ".") {
      seafloor_new[east_idx[i, 1], adjacent_col] <- ">"
      seafloor_new[east_idx[i, 1], east_idx[i, 2]] <- "."
    }
  }
  return(seafloor_new)
}

move_south <- function(seafloor) {
  south_idx <- which(seafloor == "v", arr.ind = TRUE)
  
  seafloor_new <- seafloor
  for (i in 1:nrow(south_idx)) {
    # Find the adjacent space (one row down)
    adjacent_row <- south_idx[i, 1] + 1
    # If off the bottom edge of the map, back to the top
    if (adjacent_row > max_row) {
      adjacent_row <- adjacent_row - max_row
    }
    # If unoccupied, move it
    if (seafloor[adjacent_row, south_idx[i, 2]] == ".") {
      seafloor_new[adjacent_row, south_idx[i, 2]] <- "v"
      seafloor_new[south_idx[i, 1], south_idx[i, 2]] <- "."
    }
  }
  return(seafloor_new)
}

Repeat steps in a loop until the matrix isn’t changing:

step <- 0
repeat {
  step <- step + 1
  seafloor_new <- seafloor %>% move_east() %>% move_south()
  
  # If the map hasn't changed, break
  if (all(seafloor_new == seafloor)) break
  seafloor <- seafloor_new
}
step

[1] 507

Part 2

Suddenly, the experimental antenna control console lights up:

Sleigh keys detected!

According to the console, the keys are directly under the submarine. You landed right on them! Using a robotic arm on the submarine, you move the sleigh keys into the airlock.

Now, you just need to get them to Santa in time to save Christmas! You check your clock - it is Christmas. There’s no way you can get them back to the surface in time.

Just as you start to lose hope, you notice a button on the sleigh keys: remote start. You can start the sleigh from the bottom of the ocean! You just need some way to boost the signal from the keys so it actually reaches the sleigh. Good thing the submarine has that experimental antenna! You’ll definitely need 50 stars to boost it that far, though.

The experimental antenna control console lights up again:

Energy source detected.
Integrating energy source from device "sleigh keys"...done.
Installing device drivers...done.
Recalibrating experimental antenna...done.
Boost strength due to matching signal phase: 1 star

Only 49 stars to go.

If you like, you can [Remotely Start the Sleigh Again].

Thankfully I solved all the puzzles in order, and so immediately had all 49 stars required to get the 50th. Clicking on the remote start link reveals the end page:

You use all fifty stars to boost the signal and remotely start the sleigh! Now, you just have to find your way back to the surface…

…did you know crab submarines come with colored lights?

Congratulations! You’ve finished every puzzle in Advent of Code 2021! I hope you had as much fun solving them as I had making them for you.

Stats and conclusions

Here are my personal stats for these last 5 days:

tibble::tribble(
  ~Part, ~Day, ~Time, ~Rank,
  1, 25, ">24h", 11179,
  2, 25, ">24h", 6765,
  1, 24, ">24h", 8152, 
  2, 24, ">24h", 8018,
  1, 23, ">24h", 9585, 
  2, 23, ">24h", 6847,
  1, 22, "12:44:05", 12908,
  2, 22, "23:02:28", 8867,
  1, 21, "09:40:13", 14341,
  2, 21, "11:35:27", 9163
) %>%
  pivot_wider(names_from = Part, values_from = c(Time, Rank),
              names_glue = "Part {Part}_{.value}") %>%
  mutate(
    `Time between parts` = as.numeric(hms(`Part 2_Time`) - hms(`Part 1_Time`),
                                      "minutes") %>% round(1)
  ) %>%
  gt() %>%
  tab_spanner_delim(delim = "_", split = "first") %>%
  sub_missing(columns = "Time between parts", missing_text = "")

Day	Time		Rank		Time between parts
Day	Part 1	Part 2	Part 1	Part 2	Time between parts
25	>24h	>24h	11179	6765
24	>24h	>24h	8152	8018
23	>24h	>24h	9585	6847
22	12:44:05	23:02:28	12908	8867	618.4
21	09:40:13	11:35:27	14341	9163	115.2

I really lagged behind in the last few days, mostly due to work and family time around Christmas, but I also found the puzzle difficulty ramped up a lot. This is probably a similar story to others on the private leaderboard:

library(httr)

leaderboard <- httr::GET(
  url = "https://adventofcode.com/2021/leaderboard/private/view/1032765.json",
  httr::set_cookies(session = Sys.getenv("AOC_COOKIE"))
) %>%
  content() %>%
  as_tibble() %>%
  unnest_wider(members) %>%
  arrange(desc(local_score)) %>%
  transmute(
    Rank = 1:n(), Name = name, Score = local_score, Stars = stars
  )

leaderboard %>%
  gt() %>%
  text_transform(
    locations = cells_body(columns = Stars),
    fn = function(stars_col) {
      map_chr(stars_col,
              ~html(paste0(.x, fontawesome::fa('star', fill = 'gold'))))
    }
  ) %>%
  cols_align("left") %>%
  tab_style(
    style = list(cell_text(weight = "bold")),
    locations = cells_body(
      rows = (Name == "taylordunn")
    )
  ) %>%
  tab_options(container.height = 500)

Rank	Name	Score	Stars
1	Colin Rundel	6386	50
2	@ClareHorscroft	6280	50
3	trang1618	6269	50
4	Ildikó Czeller	6156	50
5	pritikadasgupta	5858	50
6	David Robinson	5846	46
7	Anna Fergusson	5726	50
8	ashbaldry	5516	50
9	Tom Jemmett	5485	50
10	Jean-Rubin	4955	45
11	Josh Gray	4892	44
12	Darrin Speegle	4724	50
13	taylordunn	4717	50
14	mbjoseph	4436	44
15	@_TanHo	4433	36
16	dhimmel	4427	36
17	@Mid1995Sed	4377	43
18	Jim Leach	4233	44
19	Riinu Pius	4172	40
20	Jonathan Spring	4159	36
21	Calum You	4138	42
22	Jarosław Nirski	3990	34
23	TJ Mahr	3899	44
24	Emil Hvitfeldt	3836	30
25	Melinda Tang	3363	32
26	gpecci	3184	27
27	jordi figueras puig	3099	33
28	fabio machado	3019	30
29	Jaap Walhout	2959	32
30	patelis	2936	32
31	Farhan Reynaldo	2849	30
32	KT421	2809	32
33	martigso	2784	32
34	john-b-edwards	2775	24
35	hrushikeshrv	2762	27
36	long39ng	2747	32
37	AlbertRapp	2619	31
38	Sherry Zhang	2615	24
39	@_mnar99	2597	24
40	Tokhir Dadaev	2573	27
41	Aron Strandberg	2569	30
42	Dusty Turner	2445	33
43	@E_E_Akcay	2355	26
44	Doortje Theunissen	2344	28
45	Andrew Argeros	2265	22
46	Nathan Moore	2199	26
47	Jacqueline Nolis	2122	17
48	Matt Onimus	2106	26
49	mkiang	2019	17
50	duju211	2005	27
51	scalgary	1962	24
52	Derek Holliday	1925	18
53	Kelly N. Bodwin	1842	22
54	delabj	1830	22
55	Jenna Jordan	1797	28
56	Flavien Petit	1784	21
57	CarlssonLeo	1763	23
58	HannesOberreiter	1740	18
59	Jeffrey Brabec	1641	22
60	Alex N	1498	17
61	rywhale	1467	20
62	Daniel Coulton	1440	18
63	@woodspock	1433	17
64	Zach Bogart 💙	1402	14
65	karawoo	1382	15
66	Erez Shomron	1364	20
67	blongworth	1353	21
68	Arun Chavan	1343	17
69	TylerGrantSmith	1269	17
70	exunckly	1254	15
71	Scott-Gee	1193	17
72	Nerwosolek	1140	16
73	pi55p00r	1082	15
74	Ghislain Nono Gueye	972	14
75	Miha Gazvoda	924	14
76	cramosu	902	10
77	cathblatter	860	13
78	mfiorina	839	15
79	Sydney	821	11
80	A-Farina	793	15
81	MetaMoraleMundo	775	7
82	@mfarkhann	760	15
83	jwinget	753	15
84	Andrew Tungate	710	15
85	collinberke	687	8
86	ldnam	663	6
87	Eric Ekholm	635	11
88	cynthiahqy	623	14
89	dirkschumacher	619	10
90	Adam Mahood	616	6
91	Gypeti Casino	599	12
92	Maya Gans	589	11
93	antdurrant	568	9
94	David Schoch	551	6
95	Julian Tagell	473	5
96	AmitLevinson	473	7
97	Josiah Parry	454	7
98	thedivtagguy	436	6
99	andrew-tungate-cms	421	6
100	@Maatspencer	409	8
101	@KentWeyrauch	404	8
102	Wendy Christensen	391	6
103	Emryn Hofmann	390	7
104	columbaspexit	382	8
105	ALBERT	377	4
106	Alan Feder	345	6
107	Kevin Kent	335	7
108	olmgeorg	327	6
109	Daniel Gemara	302	4
110	quickcoffee	282	6
111	Andrew Fraser	248	3
112	soto solo	244	3
113	jennifer-furman	242	4
114	Adrian Perez	216	4
115	Billy Fryer	209	5
116	April	197	2
117	Lukas Gröninger	173	4
118	Kyle Ligon	166	6
119	Duncan Gates	129	5
120	Jose Pliego San Martin	125	2
121	aleighbrown	118	2
122	Bruno Mioto	98	3
123	chapmandu2	64	4
124	@jdknguyen	36	3
125	Matthew Wankiewicz	20	1
126	CaioBrighenti	0	0
127	Wiktor Jacaszek	0	0
128	jacquietran	0	0
129	Rizky Luthfianto	0	0
130	Tony ElHabr	0	0
131	NA	0	0

13th place out of 130, which I’m very happy with, especially since the puzzles released at 1AM my time so I generally didn’t get to start until after work the next day.

My main takeaways, which may help me in future years of Advent of Code:

Read the full puzzle instruction.
Don’t be afraid of base R. As a huge tidyvese advocate, I found some problems much easier to approach with base R, especially the matrix class.
That being said, wow does my pandas code feel more cumbersome/ugly compared to the tidyverse equivalent (though this may just be because I am much more experienced with the latter).
When a problem seems like it will take too long to run, consider these in order:
- keeping track of unique states, rather than each state individually,
- parallelization with future and furrr, and
- memoization (caching the result of computationally expensive functions).
Read the full puzzle instruction.
Joining a private leaderboard makes for great motivation. I really enjoyed “competing” in Tan Ho’s leaderboard – “competing” in quotes because it served more as a place to complain and help each other via the R for Data Science Slack group.

Reproducibility

Session info

 setting  value
 version  R version 4.2.1 (2022-06-23 ucrt)
 os       Windows 10 x64 (build 19044)
 system   x86_64, mingw32
 ui       RTerm
 language (EN)
 collate  English_Canada.utf8
 ctype    English_Canada.utf8
 tz       America/Curacao
 date     2022-10-27
 pandoc   2.18 @ C:/Program Files/RStudio/bin/quarto/bin/tools/ (via rmarkdown)

python:         C:/Users/tdunn/Documents/.virtualenvs/r-reticulate/Scripts/python.exe
libpython:      C:/Users/tdunn/AppData/Local/r-reticulate/r-reticulate/pyenv/pyenv-win/versions/3.9.13/python39.dll
pythonhome:     C:/Users/tdunn/Documents/.virtualenvs/r-reticulate
version:        3.9.13 (tags/v3.9.13:6de2ca5, May 17 2022, 16:36:42) [MSC v.1929 64 bit (AMD64)]
Architecture:   64bit
numpy:          C:/Users/tdunn/Documents/.virtualenvs/r-reticulate/Lib/site-packages/numpy
numpy_version:  1.23.3

NOTE: Python version was forced by use_python function

Git repository

Local:    main C:/Users/tdunn/Documents/tdunn-quarto
Remote:   main @ origin (https://github.com/taylordunn/tdunn-quarto.git)
Head:     [4eb5bf2] 2022-10-26: Added font import to style sheet

Source code, R environment

Reuse

https://creativecommons.org/licenses/by/4.0/

Citation

BibTeX citation:

@online{dunn2021,
  author = {Dunn, Taylor},
  title = {Advent of {Code} 2021: {Days} 21-25},
  date = {2021-12-21},
  url = {https://tdunn.ca/posts/2021-12-21-advent-of-code-2021-days-21-25},
  langid = {en}
}

For attribution, please cite this work as:

Dunn, Taylor. 2021. “Advent of Code 2021: Days 21-25.” December 21, 2021. https://tdunn.ca/posts/2021-12-21-advent-of-code-2021-days-21-25.